グラフの割り算01

与えられた初等関数 \( f(x) \) (多項式、分数関数、三角関数、指数関数、対数関数などの組合せ)に対して、\(y=f(x) \) のグラフを描くとき、脊髄反射的に微分して増減表、、、としていた私へ。

増減表の前にやるべきことがたくさんあります。いや、増減表を書くまえにやれる工夫の質と量こそが数理能力の高さを示している気がします。

さて、細かい微分計算などを行うまえにやるべきこと。それは、知っている基本的な曲線の組合せで概形を描いてしまうこと。

二つのグラフを足す、引く（＝-1倍して足す＝x軸に対して上下反転させて足す）、掛けるは、だいたい想像がつくので後回し。

もっとも微分との相性の悪い（微分すればするほど汚くなる）、分数関数の描き方のコツから。

グラフの割り算とは、逆数のグラフをかけ算すればいいので、逆数のグラフを描くためのコツを把握。
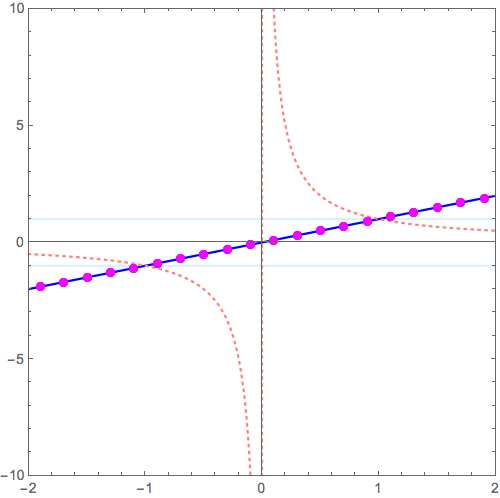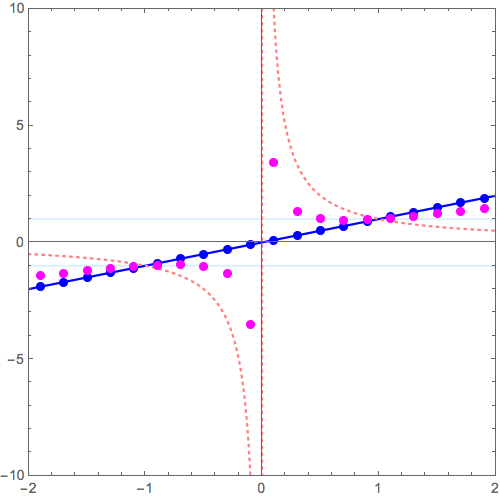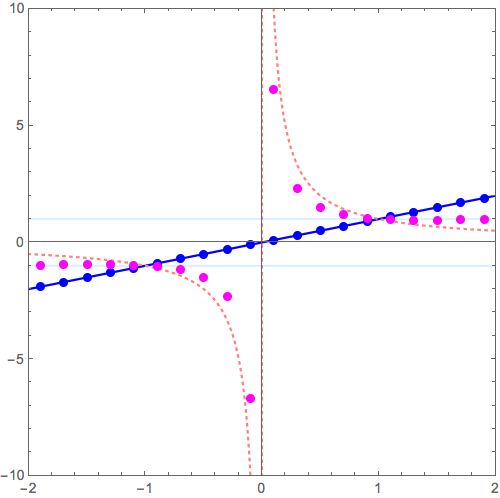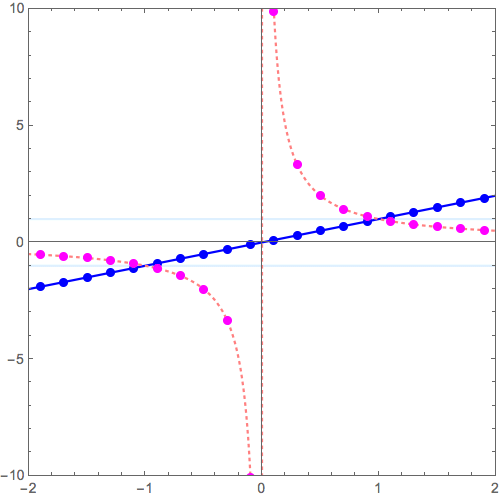
\( y = f(x) \) のグラフから\( y = 1/f(x)\)へと変形させるコツが分かれば充分。

最も簡単な \( f(x) =x \) の場合、つまり
$$ y = x \to y = \frac{1}{x}$$
を考えてみましょう。

• 逆数操作をすると
  • \( y = \pm 1 \) 上の点は不変。その近傍はあまり動かない
  • 増減が逆転する（右肩上がり、下がりが入れ替わる）
    • 原点近傍は激しく天地へと突き抜ける
    • 遠方はx軸にへばりつく

こういったこと念頭に、下記動画を眺めてみて下さい　(2017/12/02修正：点列を原点対称に微調整)。