分数関数と漸近曲線のグラフを眺めてみましょう。
$$ y=\frac{1}{x}, y=x+\frac{1}{x}, y=x^2+\frac{1}{x}, y=x^3+\frac{1}{x}, \cdots $$
といったグラフを考えます。
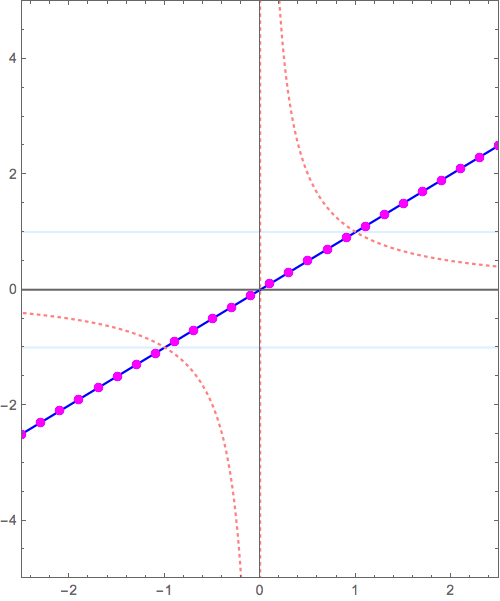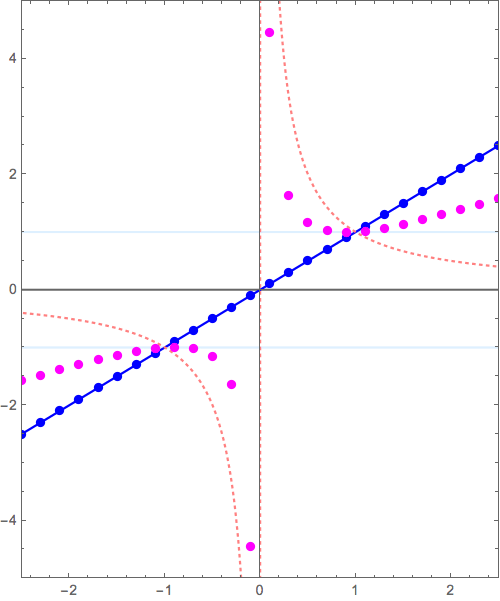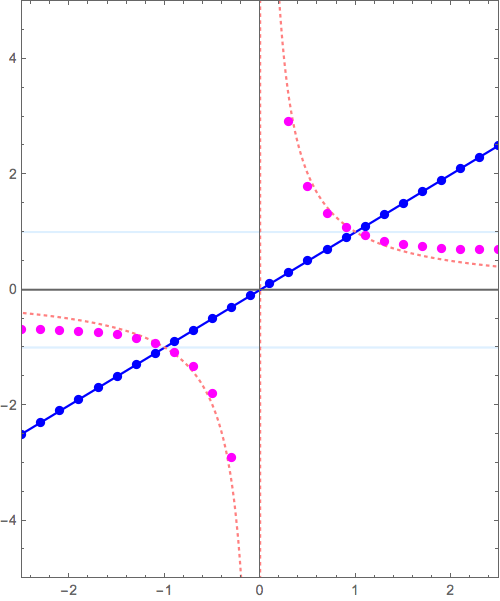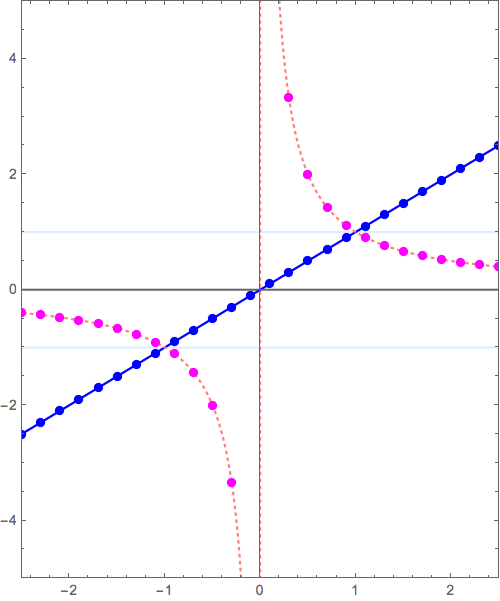
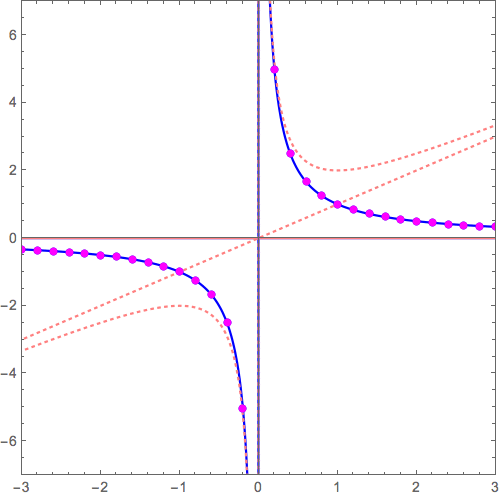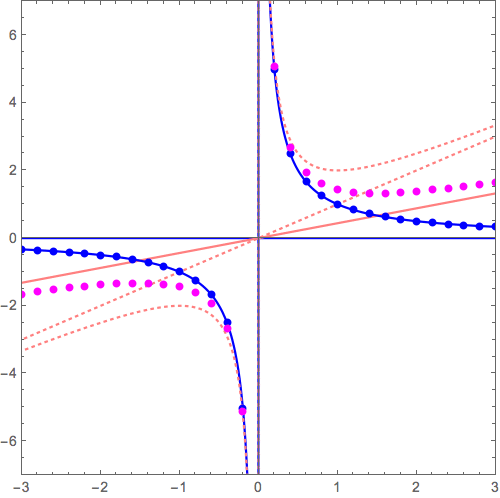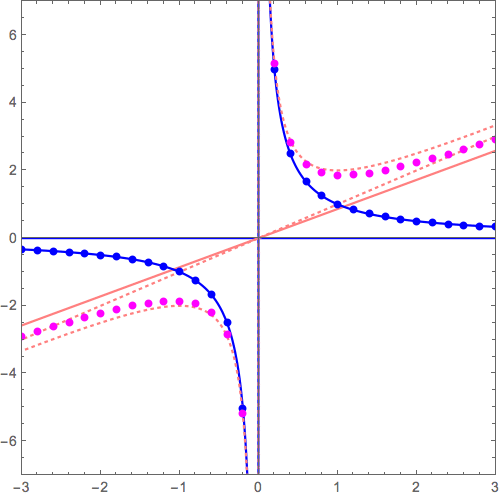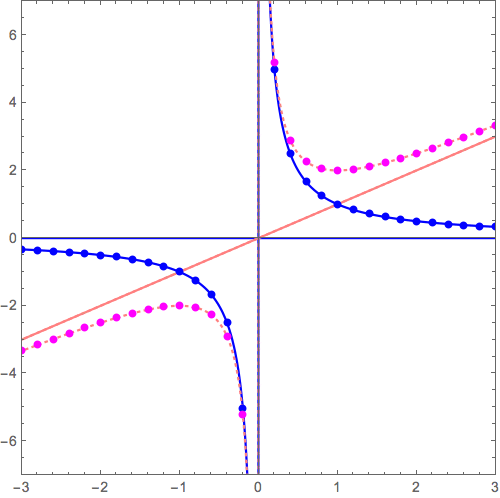
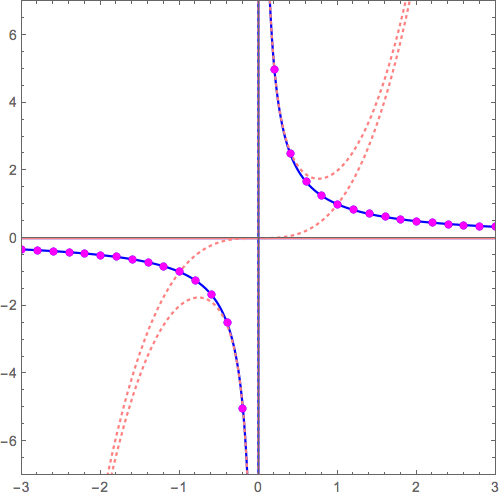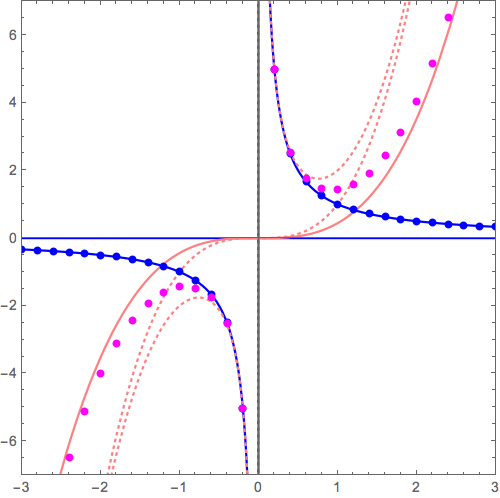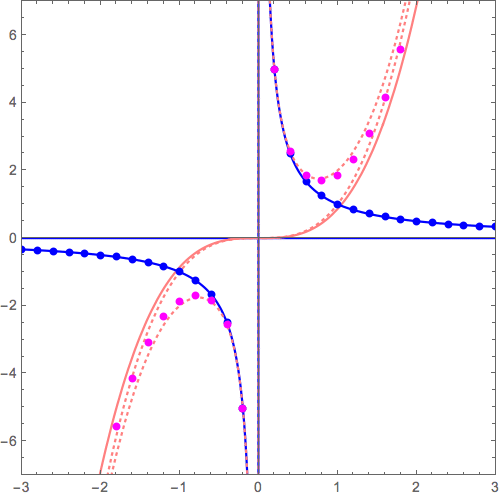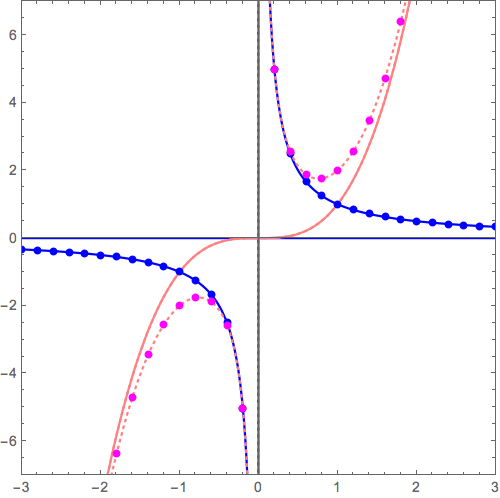
\( y=\frac{1}{x} \)のグラフ(このグラフを\( y=x \to y=\frac{1}{x}\)のように逆数グラフとして描く方法については下記もしくはこちらの記事)は、
$$y=\frac{1}{x} \longrightarrow y=0+\frac{1}{x} $$
のように、「0」つまり「x軸:\( y = 0 \)」という漸近線が隠れていると考えます。
このxy平面がゴムかなにかやわらかいものでできていると想像し、この漸近線\( y= 0 \)が別の漸近線 \( y=x, y=x^2, y=x^3, \cdots \)に重なるように「グニャッ」と変形すると\( y=x+\frac{1}{x} \), \( y=x^2+\frac{1}{x} \), \( y=x^3+\frac{1}{x}, \cdots \)ができあがります。
\( y= 0+ \frac{1}{x} \) から \( y= x+ \frac{1}{x} \) へ (2017/12/07 更新: 余韻アリ動画に差し替え。このほうが、バシッと決まる器械体操の着地みたいでイイ。)
\( y= 0+ \frac{1}{x} \) から \( y= x^2+ \frac{1}{x} \) へ
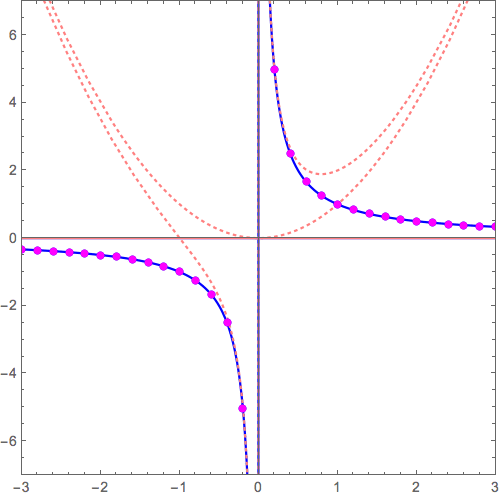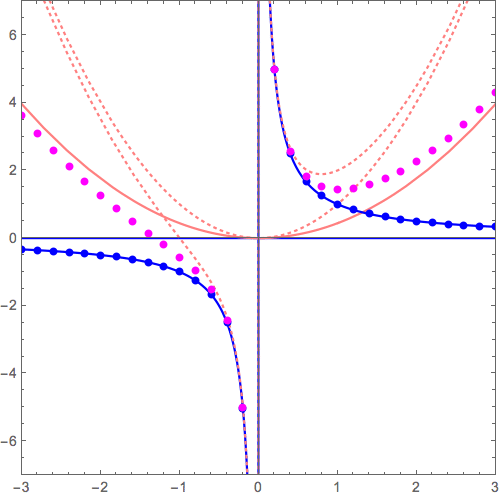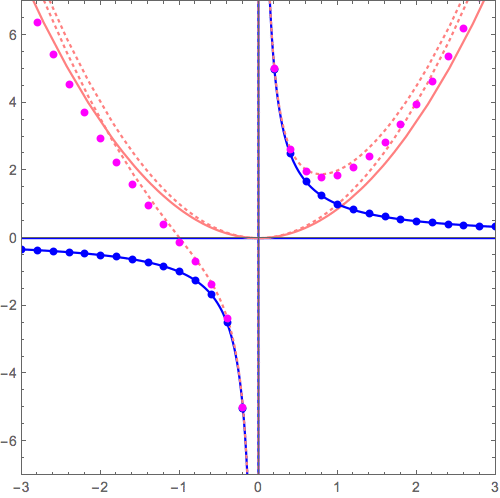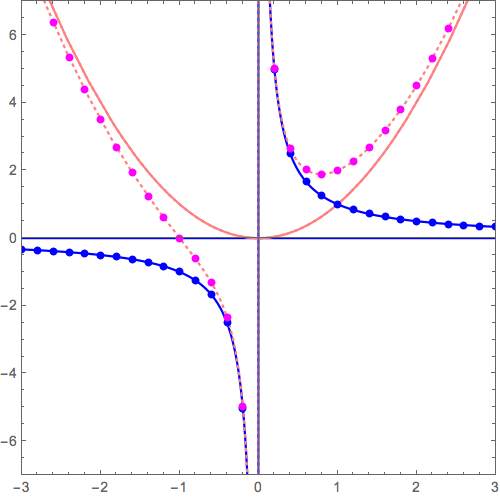
\( y= 0+ \frac{1}{x} \) から \( y= x^3+ \frac{1}{x} \) へ
参考:\(y=x \)から\( y=\frac{1}{x} \)へ