ここは『相対論とゲージ場の古典論を噛み砕く』(現代数学社, 2019年5月)のサポートページです。
まえがきから
本書では、古典力学や電磁気学や量子力学、線型代数やベクトル解析を聞きかじったことのある読者を対象に、現代物理学における相対論とゲージ理論の考え方の基本を、微分形式やリー代数の初歩といった数学を交えながら紹介します。特殊相対論とローレンツ群の表現、変分原理と解析力学、ゲージ対称性、多脚場とスピン接続といったトピックについて、その本格的な扱いや詳細に立ち入ることなく、ざっくりとその気持ちが伝わるような、軽めの解説をしました。これらを一通り目を通して頂くことで、現代物理学の標準言語である「ゲージ場の量子論」を学ぶための心の準備ができることを目指しています。
現代物理学の最重要概念の一つが場の量子です。素粒子や、物質中の微視的な現象は、場の量子を用いて記述します。場の量子を駆使する一連の基礎理論体系は場の量子論と呼ばれ、私たちが直接見たりさわったりできないようなミクロの世界のさまざまな現象をあたかも数式を通じて「見たりさわったり」できるようにする、強力な「可視化ツール」であり、現代物理学の標準言語です。
場の量子論のなかでも特に局所的な連続変換に対して理論が不変となるような特徴を備えている理論がゲージ場の量子論です。素粒子とその相互作用を記述する標準模型はゲージ場の量子論の一例です。また、物質中の量子多体現象を記述する理論としても様々なタイプのゲージ場の量子論が知られています。
本格的に理論物理学に取り組む多くの人にとっては、ゲージ場の量子論を自分なりに咀嚼して使いこなすことが大きな目標となります。ところが、通常の理工系大学の学部向けの物理学の講義や教科書を学ぶだけでは、そもそもこのゲージ場の量子論の存在を知ることすら叶わないのではないでしょうか。少なくとも私自身は、ゲージ場の量子論が大きな目標であるということを知るまでには、色んな本を買い漁っては解読に挫折、紆余曲折し、迷走に迷走を重ねました。
そこで本書は、迷走を重ねていた過去の私と似たような状況に陥っている方々を主な想定読者として、ゲージ場の量子論に至るまでのガイドブックとなることを目指しました。ここではゲージ場の量子論自体は取り扱わず、特殊相対論とローレンツ群の表現、変分原理と解析力学、ゲージ対称性、多脚場とスピン接続といった内容の本格的な取り扱いは、すべて参考文献に丸投げしてあります。
かつての私は、なかなか簡単にはたどり着けなかった情報を得るたびに「この情報をもっと早く知っていれば、もっともっと理論物理学の勉強が捗ったのに…」と苦い思いをし、その度に「タイムスリップして過去の私に伝えたいリスト」を作り温めてきました。それらは、学位取得直後のポスドク1年時にお誘い頂いた、月刊誌「理系への数学」の連載記事「数学で噛み砕く特殊相対論」(2009年5月号から2010年4月号)で取り上げました。当時、連載記事を単行本化するというお話もいただいたのですが、ちょうどその頃、ハドロン理論から物性理論へと異なる分野へと転向することが決まり、右も左も分からない新分野へ順応するまではと、単行本化の作業は一旦保留にさせて頂いていました。それから9年が経ち、物性理論研究に取り組むなか、迷走に迷走を重ねて続けて、新たな「過去の私に伝えたいリスト」が増えました。学生の頃の私、物性理論研究者の私、それぞれの「早く知りたかった」トピックを整理し直したものが本書です。
連載当時、記事として取り上げようと調べたものの、紙面の都合上割愛したトピックに、多脚場とスピン接続があるのですが、図らずも、このときに得た知識で分野転向直後に取り組んだ問題を解決できたという幸運に恵まれました。かつて「過去の私」に向けて取り組んだ作業が、「未来の私」にとって重要な支えとなったのです。そうした経緯もあり、私自身の深い思い出もかみしめながら、このトピックも本書に盛り込みました。
また、物性分野に移ってからは様々なバックグラウンドをもった理論家、実験家の方と共同研究をしてきましたが、その過程で「ゲージ場の理論ってよく耳にするけど、まとまった勉強をしたことがない。せめて気持ちだけでも知ることができたら、理論の文献が読みやすくなるのだけど…」という相談がちょくちょくありました。その都度、上述の連載記事を紹介しつつ、連載記事には書いていないトピックで、私が物性研究で使っているものを補うような即席・速習講座を開いたりしました。そうした経験からも、ゲージ場の量子論の本格的な内容は他書に丸投げのガイドブックスタイルという本書は、(特に素粒子系の教育を受けていない)研究者の方にも楽しんでいただけるのではないかと期待しています。
本書で取り上げた内容に興味がわいて、本格的な取り扱いを学びたい方は、今後の学習の参考となるような、オススメの文献を紹介してありますので、ぜひそちらに取り組んで頂けると幸いです。
目次と索引 (190415現在)
最終章から
13章(最終章) ゲージ場の量子論への道
ゲージ場の量子論を学ぶ際におすすめの本やちょっとしたコツ(?)を紹介しておきます.
ゲージ場の量子論に関する本格的な教科書としては例えば,
九後汰一郎「ゲージ場の量子論 I・II」(培風館)
S.ワインバーグ「場の量子論」(吉岡書店)
がありますがいずれも非常に手強い本です.いずれも早い段階でローレンツ群の表現やポアンカレ群の表現についての詳細な記述があり,私自身も心の準備ができないままその箇所を読もうとしてその敷居の高さに圧倒されるということがありました.その度に本書で紹介してきた文献を眺め,手を動かしたりした後に再チャレンジするということを繰り返しながら少しずつ本格的な内容に馴染んできましたし,今でも勉強を続けています.私自身の悪い癖でもあるのですが,ついつい抽象的な議論の表面だけをなぞってどんどん次のページへと急いでしまったがために,本を閉じてまっさらなノートに向かって教科書に書かれていた内容を再現しようとしても何も思い出せないという苦い経験がしょっちゅうあります.そんな私に「ちゃんと手を動かしなさい」と諭してくれるかのうような極めつけに親切な本が,すでに何度も紹介してきた
川村嘉春「相対論的量子力学」(裳華房)
坂本眞人「場の量子論–不変性と自由場を中心にして–」(裳華房)
です.ソラで数式がすらすらと再現できないときにはこの2冊の信じられないほど親切な解説に立ち返り,具体例についてたっぷりと手を動かしてみるのが良いと思っています(これは私への戒めでもあります).
物理学書に対してのみならず(というよりも輪を掛けて)数学書に関しても具体例に対して手を動かし足りない私にとっての心強い味方は
長谷川浩司「線型代数[改訂版]」(日本評論社)
藤岡敦「具体例から学ぶ多様体」(裳華房)
です.いずれも初学書に配慮した非常に親切丁寧な解説はもちろんのこと,線型代数や多様体を学ぶことでどのような世界が広がるのかを知ることができるように,楽しい応用例が紹介されています.ゲージ場の量子論に取り組むにあたり,数学的な内容で不安を感じたらまずはこれらの本にあたって,具体例で手を動かしてみるというのがとても有用だと最近もひしひしと感じています.
きっと私のように「手を動かし足りないタイプ」の読者の方にとってはここに挙げた4冊は強力な味方となってくれるはずだと思っています.
高度な本の序章をチラ見
ここまで様々な文献を紹介してきましたが,どんな文献であれ解読作業はなかなか進まないものです.取り組んでいるトピックをこの先どのように使って行くのだろうか,といった「先の見えない不安感」に襲われることがないでしょうか.そんなときに私がよくやる裏技的専門書の読み方があります.それは
《 現在解読しづらいと感じている本よりも,さらに高度な本を探し求め,その高度な本の序章にあるまとめを眺める》
というものです.
多様体を学ぶ際に多様体の入門書だけを読むのではなく,例えば小林昭七「接続と微分幾何とゲージ理論」(裳華房)や茂木勇・伊藤光弘「微分幾何学とゲージ理論」(共立)の第1章を「チラ見」します.ここには第2章以降に必要な多様体の基本事項がコンパクトにまとめられています.数百ページにわたる多様体の入門書を読み進めていくと,初めのうちは読んでいくはしからどんどん前に書かれていることが頭から抜け落ちていって,なにが大切だったのか分からなくなるといったことに悩まされるのではないでしょうか.そんなときに(現実逃避がてら)高度な本の序章をチラ見すると,圧倒的なスピード感と濃縮感で重要項目を眺めることができ,さらにはどんな応用につながるのかまで知ることができるわけです.そうやって背伸びをしたあとに元の入門書に戻ると,取り組みやすくなります(私自身,こんな「チラ見」などという不真面目なことをしても良いのだろうかと後ろめたさを感じていました.ですが,現実逃避を繰り返すうちに,いつからか開き直りました.「本の中盤から終盤を解読するのにツライ」と感じたらそこで立ち止まるよりも,「より高度な本の序盤を眺める」ことで得られるものが大きいと信じて,どんどん「高度な本の序章のチラ見」を楽しむことにしています.)
私が最初にスピン接続を知ったのは一般相対論の文献でしたが,スピン接続の取り扱いは私の手持ちの一般相対論の本でもごく一部にしかなく,しかも本の後半に少しだけ書かれている程度でした.ある日,あえて藤井保憲「超重力理論入門」(産業図書)のような一見無謀(物性物理へと転向した当時の私に必要だったのは4次元時空におけるスピン接続だったのですが,「超重力理論入門」はなんと11次元時空を対象としており,一見オーバースペックに感じられました.)とも思える本を手にとり,その第1章を眺めてみるとスピン接続と重力場中のスピノル場の取り扱いが実に丁寧に解説されていて,驚いたことがあります.
かつての私のように「チラ見」に対する後ろめたさを感る方もいらっしゃるかも知れませんが,私の例が心理バリアを取り払うきっかけとなればと願っています.
最後に
最後に一つ宣伝で締めくくらせてください.本書で紹介した解析力学や微分形式はいずれも変数変換の下で不変である,とても強力な道具であることは何度も紹介しました.それでは
「微分形式を駆使した解析力学」があれば,より見通しよくゲージ理論を学べるのではないかと思った読者の方もいらっしゃるかも知れません.実際「微分形式の微分形式による微分」を駆使して定式化された解析力学として「共変解析力学」があります。(ネットで入手可能な共変解析力学のレビューとしては,中村匡「微分形式で見た電磁気学:あるいは2+1次元人の電磁気学と時空平等解析力学について」(物性研究(2002年), 79(1): p.2-42)や,中嶋慧さんの個人ページにあるレビュー(http://physnakajima.html.xdomain.jp/CAM_rev.pdf)を参照のこと.)
共変解析力学を用いると,ゲージ場の古典論の計算が劇的に簡略化されることが知られています.本書の続編として,内山龍雄「一般ゲージ場論序説」(岩波書店)で扱われている内容を共変解析力学の立場から詳述した共著本を準備中ですので,興味を持たれた方は楽しみにしていただけると幸いです.
正誤表 (最終更新 2021/02/12 10:01)
@s.komataさん、@KKenNakamuraさん、ご指摘ありがとうございました
- ページ,行:「誤」→「正」
- 主に数式の誤植
- p.7, 脚注6)4行目 \( x’_\mu \) → \( x’^\mu \)(2021-02-12 追加:@dokukinoko44 さんありがとうございました)
- p.11, 脚注17) 2行目: \( i \sinh(i\theta) = \sin\theta \) → \( \sinh(i\theta) = i \sin \theta \)
- p.16, l.8: SO(2) → SU(2)
- p.22,l.12: \( \gamma^2 (1+(v/c)^2) \) → \( \gamma^2 (1-(v/c)^2) \)
- 【2020/04/03追記】p27, l.2 γ^2 → γ
- p.29, l.6-7 とそのページの脚注11)でΔτの定義がc倍違う。p.30, l.1-4も。
- p.61 (5.12)式の2行上「\(-2\kappa, \kappa \)」→ \(2\kappa, -\kappa \)
- p.63, l.2: 式(5.16)の右辺第2項の符号はマイナス
- 【2020/04/03追記】p.63, l.3: 式(5.16)の右辺第1項 \( \dot{Q} \)→ \( \dot{Q}_i{^2} \)
- p.67, l.13: 右辺第1項を \( \phi(t, x) \) を用いて → 右辺第1項を \( \pi(t, x) \) を用いて
- p.82, l.3: 空間成分 → 時間成分
- p.83, 式(6.41): 第2辺の \( x’^{\lambda} \) → \( x^{\lambda} \)
- p.85, l.1: 3次元電流密度 \( \bf{J} \) → \( \bf{j} \)
- p.85,l.15: \( \epsilon^{0123}=-1 \)→\( \epsilon^{0123} =+1 \)
- p.85, l.9: 力学変数である4元電流密度 → 力学変数である4元電磁ポテンシャル
- p.95, l.2: \( \partial_1\) を法線ベクトルとする → \( \partial_2 \) を法線ベクトルとする
- p.95, l.5: 「\(\partial_1\) 方向に」→トル
- p.95, l.8: 矢印aが平面の集まりbを → 矢印bが平面の集まりaを
- p.104, l.6: 「ライプニッツ則」→「鎖則」
- p.110, 脚注3): \( \epsilon^{0123} = -1 \)→ \( \epsilon^{0123} = +1\)
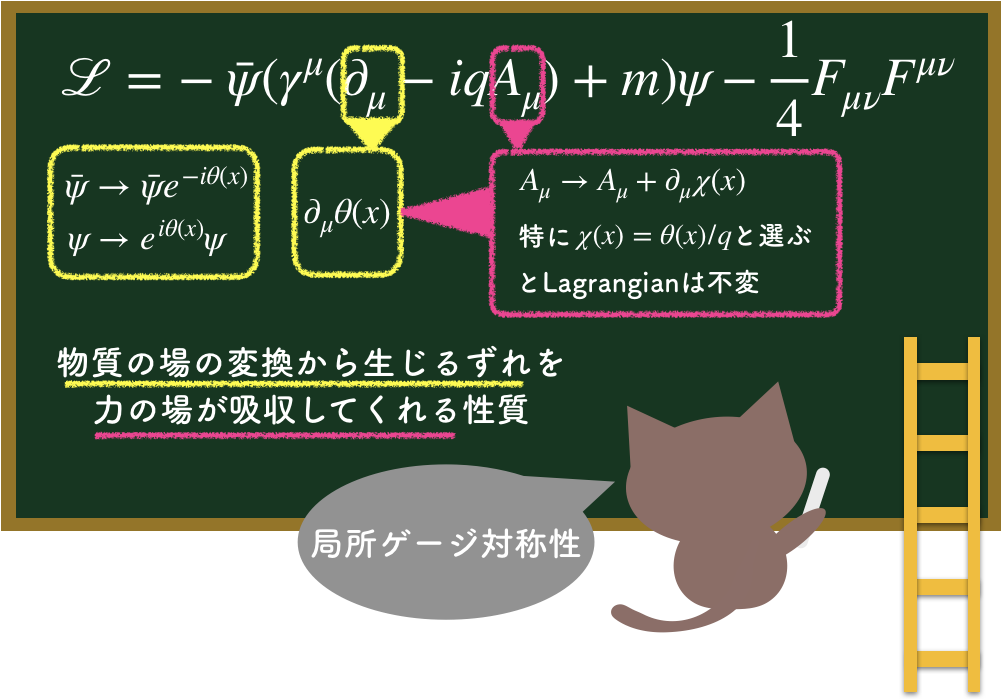
- p.137: ねこはかせの板書のγ行列の位置→ \( (\gamma^\mu \partial_\mu + m) \)
- p.142, 下から4行目の数式:\( e^{i\theta_1(x)}\cdot e^{i\theta_1(x)} \)→\( e^{i\theta_1(x)}\cdot e^{i\theta_2(x)} \)
- p.151, 式(12.13), 第2辺:\( \Omega_l\) →\( \Omega_k\)
- そのほかの誤植
- p.23, 最下行: 自動車からと → 自動車から
- p.33, l.6: 変分原理によってに → 変分原理によって
- p.42で4.5節が文の途中で唐突に終わっている→(図の配置ずれで文の最後が図に隠れてしまっていました)解析力学には「変数変換と保存則の関係」が見やすいという特長があります.
- p.58, l.9: 学ぶするのに → 学ぶのに
- p.66, l.6: 空間成分xを → 空間成分xが
- p.69, 下から2行目: 相対論的場を → 相対論的場において
- p.71, l.8: 感じ取ってもらる → 感じ取ってもらう
- p.73, 脚注6), 3行目: 具体例についての豊富な具体例→豊富な具体例を通じて
- p.76, 下から3行目: のようなもの定義する → のようなものを定義する
- p.81, l.13: 成分を見なすとき → 成分と見なすとき
- p.84, 脚注20), 3行目; p.93, 脚注9), 1行目; p.161, 37: Thone → Thorne, Gravitation の左引用符が逆向き
- p.85, l.9: 力学変数である4元電流密度 → 力学変数である4元電磁ポテンシャル
- p.86, l.8: 判断するこができます → 判断することができます
- p.88, l.3: 下付添え字 → 下付き添え字
- p.90, l.10: 変化されることで得られる → 変化させることで得られる
- p.90, 脚注5), 下から2行目: 増えていることかを → 増えているかをp.95, 脚注11): 書名 The road to reality の左引用符が逆向き
- p.104, l.16: 打ち消つし合う → 打ち消し合う
- p.106, 脚注25), 4行目: 具体的にな → 具体的な
- p.106, 脚注25), 最下行: 手を取って → 手に取って
- p.116, 脚注2), 5行目;p.130, 脚注13), 1行目; p.143, 脚注2), 4行目; p.161, 44 :「接続と微分幾何とゲージ理論」 → 「接続の微分幾何とゲージ理論」
- p.120, l.18: とな何か → とは何か
- p.121, l.19: ベクトルA(P)を → ベクトルA(P)が
- p.132, 脚注2), 3行目: 届いておおり → 届いており
- p.135, 脚注11), 4行目: 取り上がられない → 取り上げられない
- p.135, 脚注11), 最下行: Tegrad → Tetrad
- p.136, 脚注12), 3行目: 行列をみたときの → 行列とみたときの
- p.142, 下から2行目: 2つ操作 → 2つの操作
- p.143, l.1: 2つ要素 → 2つの要素
- p.157, l.18: かのうような → かのような
- p.159, l.8: 感る → 感じる
おすすめの参考文献など(本書でとりあげていないものも紹介) [随時更新中]
著者名・翻訳者名で迷わず一通り買い揃えているくらいいつもお世話になりっぱなしなのが,S. Weinbergさん,A. Zeeさん (https://www.kitp.ucsb.edu/zee),高橋康さん,須藤靖さん,樺沢宇紀さん(https://adx50150.wixsite.com/kabasawa-yakusho), 広江克彦さん (http://eman-physics.net/),小林昭七さん,横田一郎さん.
A. Zeeさんの著書
- A. Zee, “Group Theory in a Nutshell for Physicists”
- A. Zee, “Quantum Field Theory in a Nutshell”
- A. Zee, “Einstein Gravity in a Nutshell”
高橋康さんの著書
- 高橋康『量子力学を学ぶための 解析力学入門』
- 高橋康『場の解析力学入門』
- 高橋康『古典場から量子場への道』
- 高橋康『電磁気学再入門QEDへの準備』
- 高橋康『物理数学ノート』
- 高橋康『物理数学ノートII』
須藤靖さんの著書
- 須藤靖『一般相対論入門』
- 須藤靖『解析力学・量子論』
樺沢宇紀さんによる訳書
- ザゴスキン『多体系の量子論』
- M.ストーン『量子場の物理』
- Cottingham-Greenwood『素粒子標準模型入門』
- ザイマン『現代量子論の基礎』
- 坂本眞人『場の量子論』
- S.ワインバーグ『場の量子論』
- 九後『ゲージ場の量子論』
- 内山龍雄『一般ゲージ場論序説』
- 藤井保憲『超重力理論入門』
- S. Weinberg, “Gravitation and Cosmology”
- Ryder, “Introduction to General Relativity”
ウェブ上で入手可能な文献
- 国広さんの量子力学サポートページ http://www2.yukawa.kyoto-u.ac.jp/~teiji.kunihiro/QM_suppl/index_QM.html
- 本文に書ききれなかった(紙面の都合上,泣く泣く削除されたとのこと)内容の補遺がとても充実しています.
- 量子力学を学ぶための解析力学ミニマム,振動の物理学入門など,すでに学んだことのある内容についても発見が多くて勉強になります.
- 一般的な量子力学の教科書では扱われないような内容についても丁寧な解説がたっぷり.オススメです
- 坂本眞人さん「場の量子論」のサポートページ http://www2.kobe-u.ac.jp/~dragon/#intro_QFT
- 本文中の解答例と補足は,QFT自習教材として最高峰の親切丁寧さ.
- H. Tasakiさん
- http://www.gakushuin.ac.jp/~881791/mathbook/index.html
- http://www.gakushuin.ac.jp/~881791/halJ.htm#articles
- Y. Tachikawaさん https://member.ipmu.jp/yuji.tachikawa/
- 物理数学III https://member.ipmu.jp/yuji.tachikawa/lectures/2017-butsurisuugaku3/
- 量子力学II https://member.ipmu.jp/yuji.tachikawa/lectures/2016-qm2/
- Y. Matsuoさん http://www-hep.phys.s.u-tokyo.ac.jp/~matsuo/files.html
- M. Uedaさん http://cat.phys.s.u-tokyo.ac.jp/lecture/MP3_16/MP3_16.html
- G. ‘t Hooftさん
- http://www.staff.science.uu.nl/~gadda001/goodtheorist/index.html
- http://www.staff.science.uu.nl/~gadda001/goodtheorist/gr.html
- C. Popeさん
- http://people.physics.tamu.edu/pope/
- Gravitational Physics 647 http://people.physics.tamu.edu/pope/grav-phys.pdf
- Geometry and Group Theory http://people.physics.tamu.edu/pope/geom-group2006.pdf