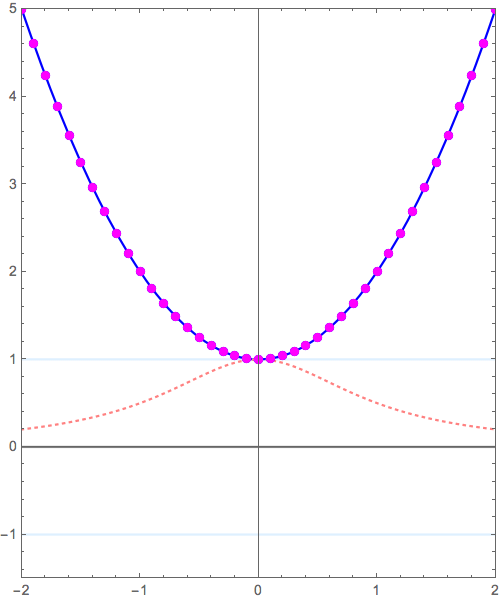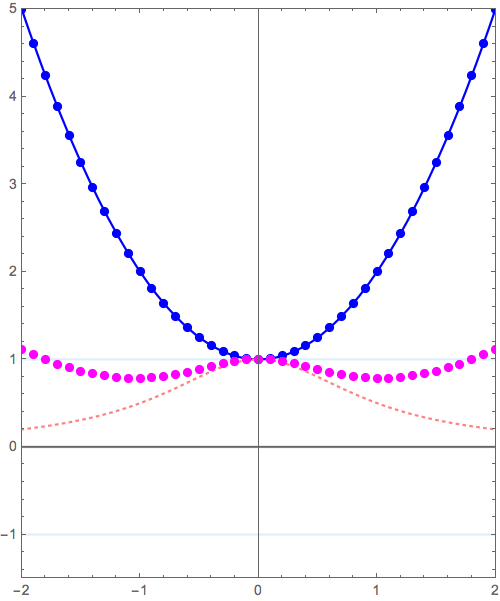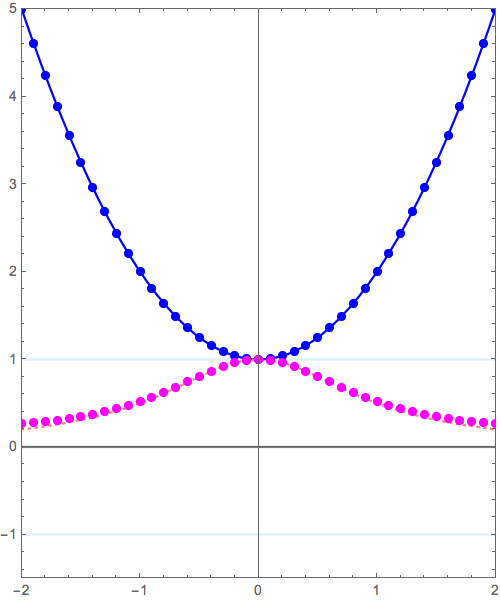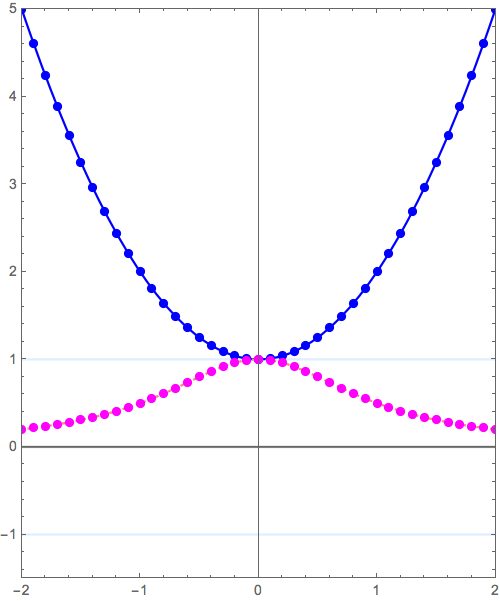
\( y = f(x) \) のグラフから\( y = 1/f(x)\)へと変形させるシリーズ。
ここまでくると、かなりのものが想像できてきます。
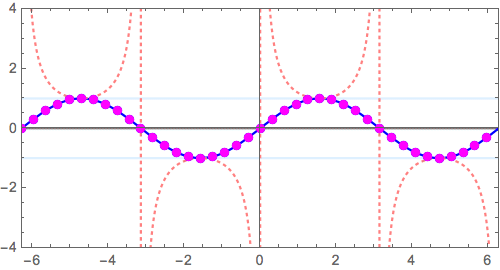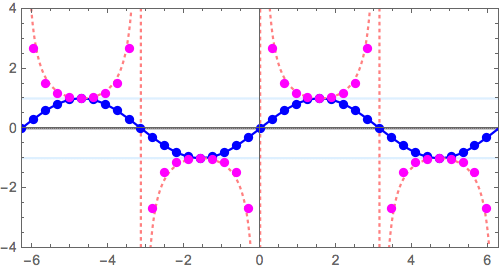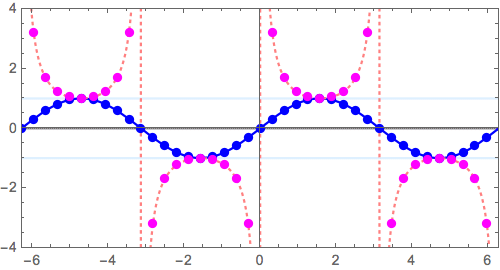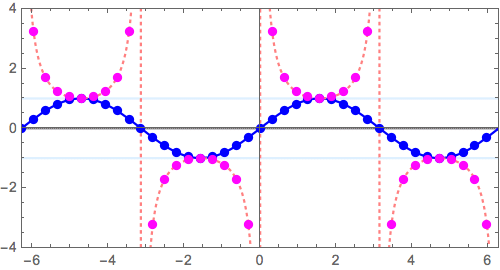
\( f(x) =\sin x \) の場合、つまり \( x =n\pi \, (n=0,\pm 1, \pm 2, \cdots ) \)でゼロ点を持つ、正弦波を「ひっくり返して」みます。
$$ y = \sin x \longrightarrow y = \frac{1}{\sin x}$$
- 逆数操作では
- \( y = \pm1 \) 上の点は不変。その近傍はあまり動かない
- 増減が逆転する(右肩上がり、下がりが入れ替わる)
- 極小点は極大点へ、極大点は極小点へ
- ゼロ点近傍
に注意します。
さらに、$$ y = \sin^2 x \longrightarrow y = \frac{1}{\sin^2 x}$$
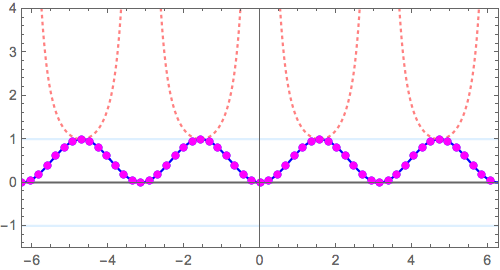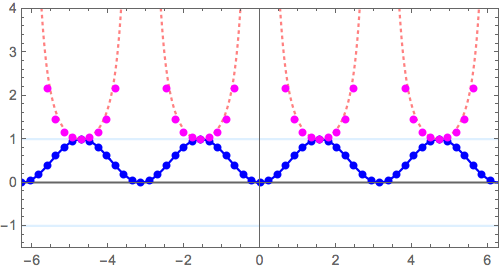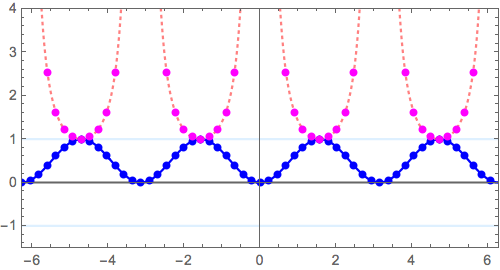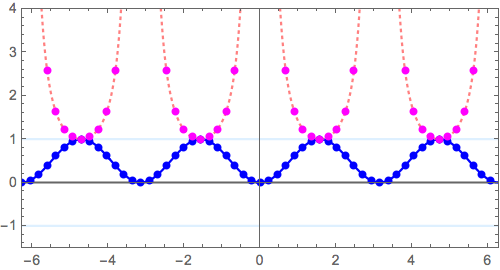
本質は、\( y=(x+2)(x-1)^2 \to y=\frac{1}{(x+2)(x-1)^2} \)につまっています。
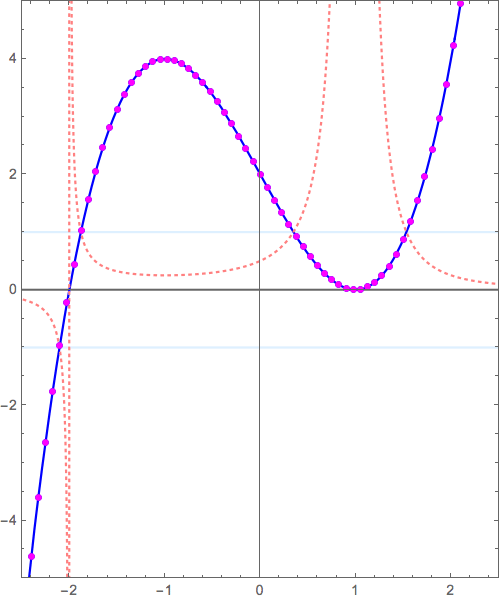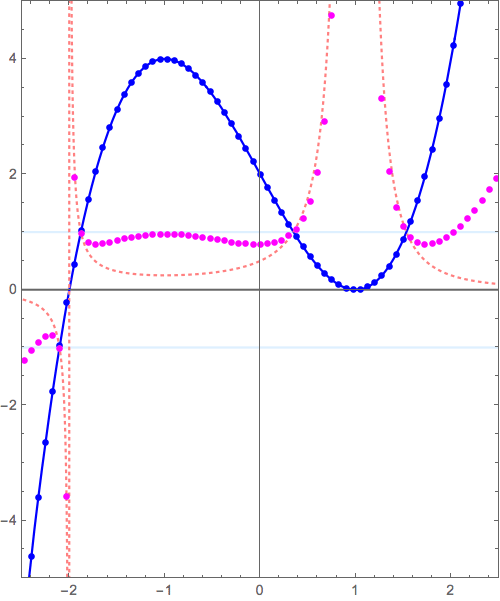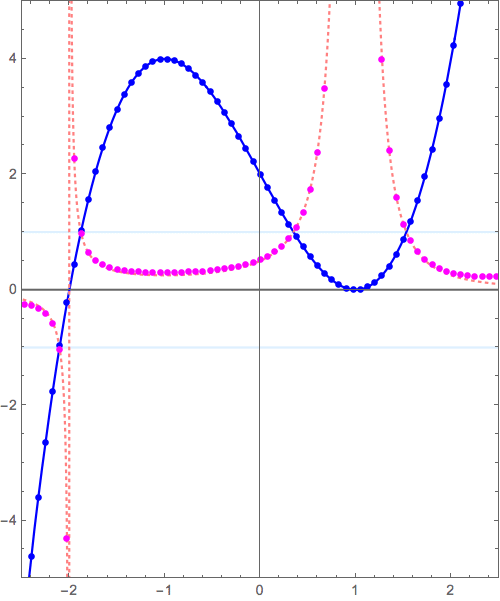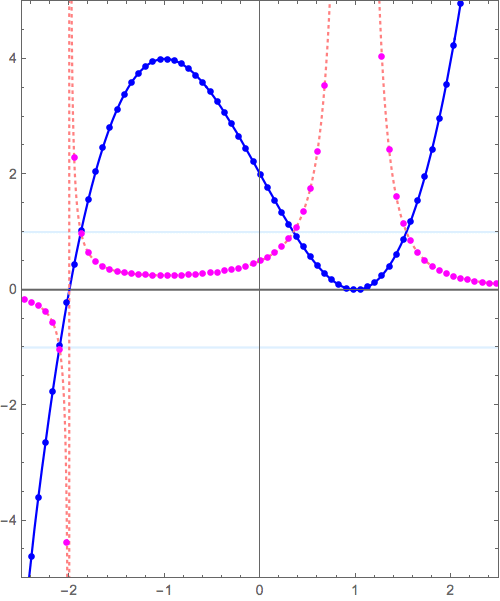
参考:
\( y = x \to y = \frac{1}{x} \) の変形
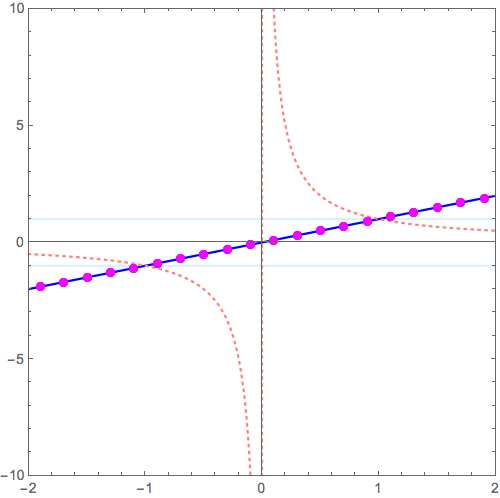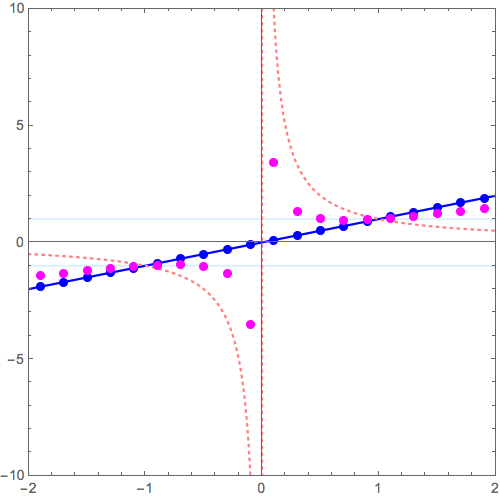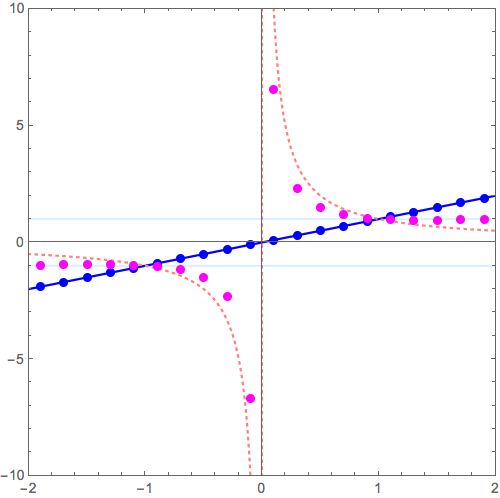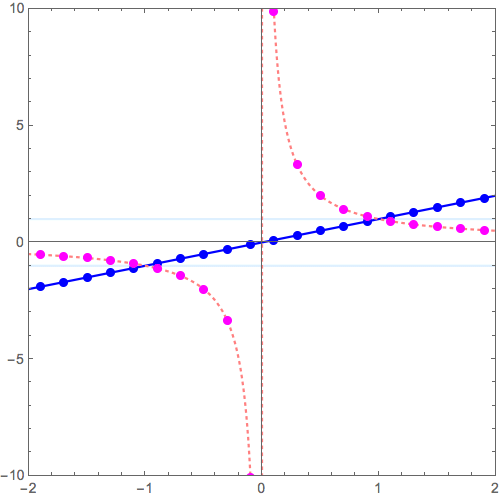
\( y = x^2 \to y = \frac{1}{x^2} \) の変形

\( y = x^2+1 \to y = \frac{1}{x^2+1} \) の変形