\( y = f(x) \) のグラフから\( y = 1/f(x)\)へと変形させるシリーズ。
\( f(x) =(x+2)(x-1)^2 \) の場合、つまり\(x=-2 \)ではx軸をまたぎ、\(x= 1 \)でx軸に接するような3次関数を「ひっくり返して」みます。
$$ y = (x +2)(x-1)^2 \longrightarrow y = \frac{1}{(x+1)(x-1)^2}$$
- 逆数操作では、
- \( y = \pm1 \) 上の点は不変。その近傍はあまり動かない
- 増減が逆転する(右肩上がり、下がりが入れ替わる)
- ゼロ点近傍の発散のしかた
- 遠方はx軸にへばりつきかた
- x軸をまたぐのか接するのか
- 極大点は極小点へ
などに気をつけてみます。下記が予測できたでしょうか。
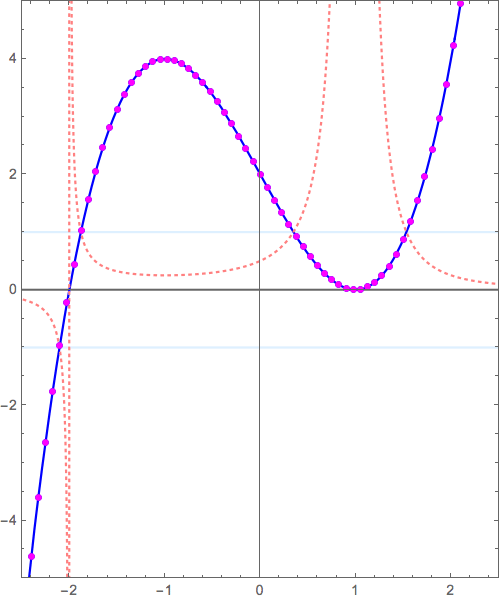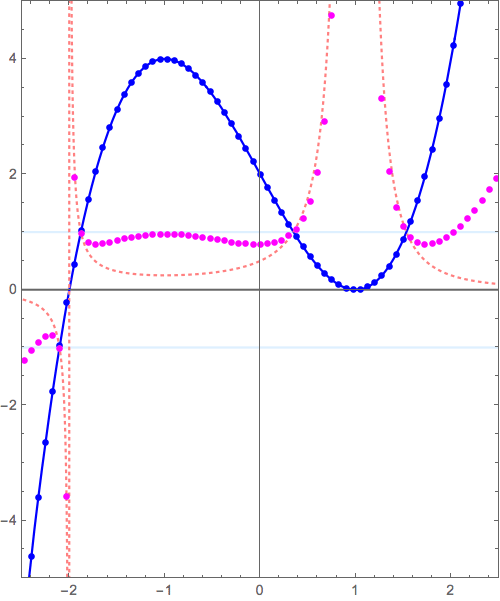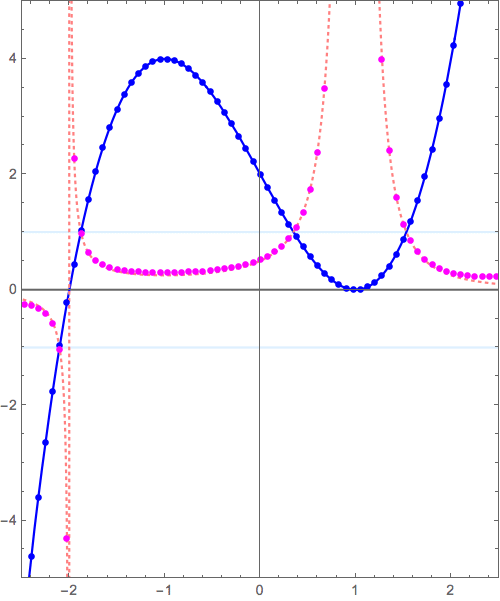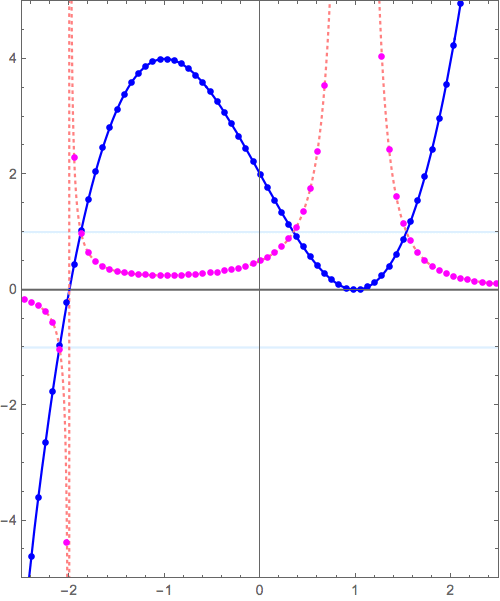
- \( x=-2 \) 付近で \( y = x \longrightarrow y = \frac{1}{x} \) の変形(の原点付近の様子)と似た状況
- \( x= 1 \) 付近で \( y = x^2 \longrightarrow y = \frac{1}{x^2} \) の変形(の原点付近の様子)と似た状況
となっています。
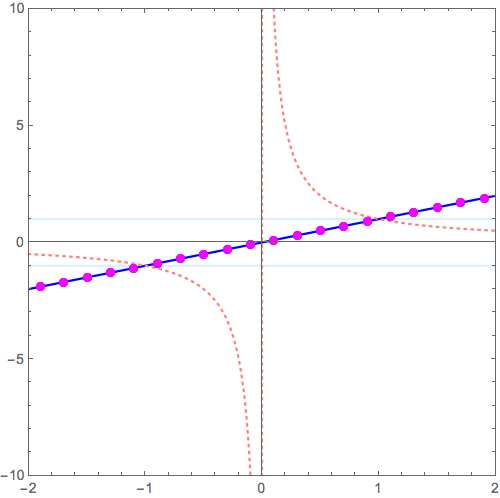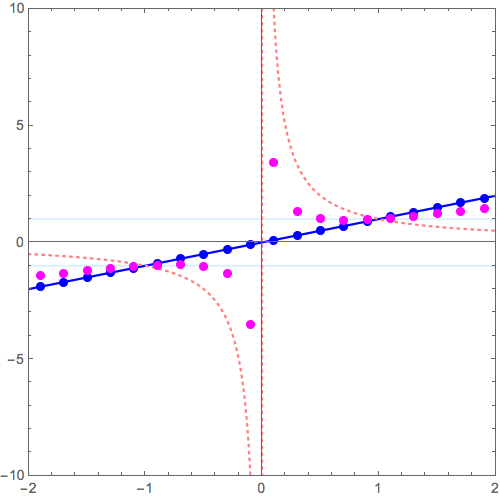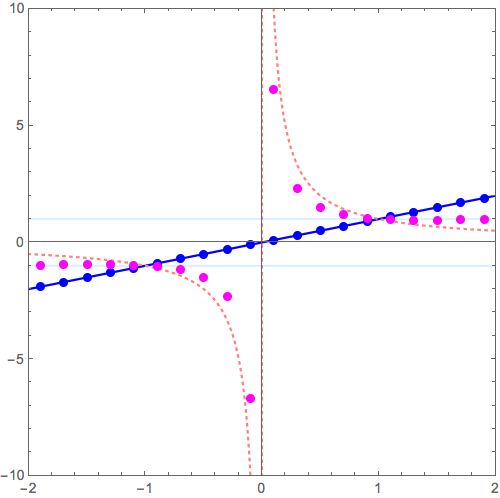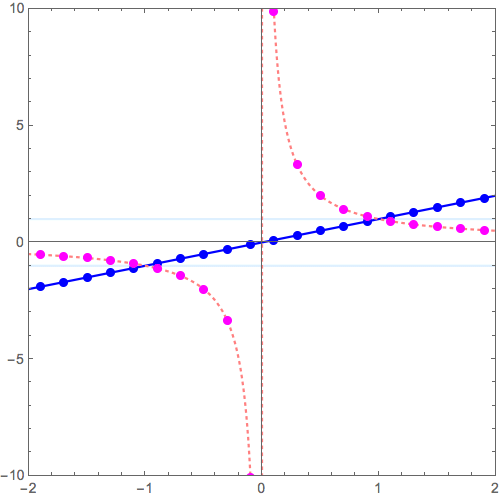
\( y = x \longrightarrow y = \frac{1}{x} \) の変形
\( y = x^2 \longrightarrow y = \frac{1}{x^2} \) の変形
